Artificial Neural Network Basics

Artificial Neural Network Basics#

Neural networks#

When we talk about machine learning, we often mean an artifical neural network. A neural network mimics the action of neurons in your brain. We’ll follow the notation from Computational Methods for Physics by Franklin.

Basic idea:

  • Create a nonlinear fitting routine with free parameters

  • Train the network on data with known inputs and outputs to set the parameters

  • Use the trained network on new data to predict the outcome

We can think of a neural network as a map that takes a set of \(N_\mathrm{in}\) parameters and returns a set of \(N_\mathrm{out}\) parameters, which we can express this as:

\[{\bf z} = {\bf A} {\bf x}\]

where

\[{\bf x} = (x_1, x_2, \ldots, x_{N_\mathrm{in}})\]

are the inputs,

\[{\bf z} = (z_1, z_2, \ldots, z_{N_\mathrm{out}})\]

are the outputs, and \({\bf A}\) is an \(N_\mathrm{out} \times N_\mathrm{in}\) matrix.

Our goal is to determine the matrix elements of \({\bf A}\).

Nomenclature#

We can visualize a neural network as:

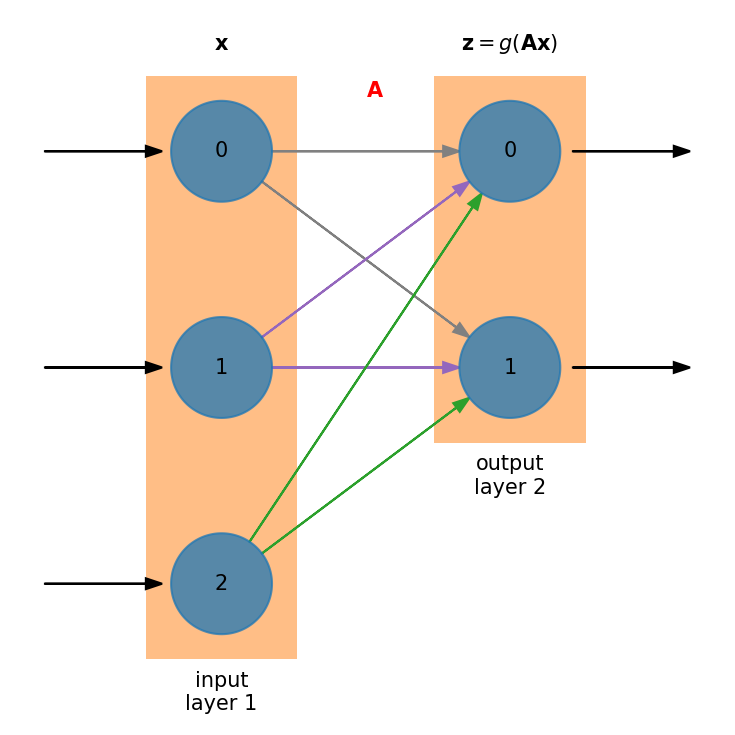
NN diagram

  • Neural networks are divided into layers

    • There is always an input layer—it doesn’t do any processing.

    • There is always an output layer.

  • Within a layer there are neurons or nodes.

    • For input, there will be one node for each input variable. In this figure, there are 3 nodes on the input layer.

    • The output layer will have as many nodes are needed to convey the answer we are seeking from the network. In this case, there are 2 nodes on the output layer.

  • Every node in the first layer connects to every node in the next layer

    • The weight associated with the connection can vary—these are the matrix elements.

      Note

      This is called a dense layer. There are alternate types of layers we can explore where the nodes are connected differently.

  • In this example, the processing is done in layer 2 (the output)

  • When you train the neural network, you are adjusting the weights connecting to the nodes

    • Some connections might have zero weight

    • This mimics nature—a single neuron can connect to several (or lots) of other neurons.

Universal approximation theorem#

A neural network can be designed to approximate any function, \(f(x)\). For this to work, there must be a source of non-linearity in the network—this is a result of the universal approximation theorem.

We use a nonlinear activation function that is applied in a layer. It has the form:

\[\begin{split}g({\bf v}) = \left ( \begin{array}{c} g(v_0) \\ g(v_1) \\ \vdots \\ g(v_{n-1}) \end{array} \right )\end{split}\]

Note

The activation function, \(g({\bf v})\) works element-by-element on the vector \({\bf v}\).

Then our neural network has the form: \({\bf z} = g({\bf A x})\)

We want to choose a function \(g(\xi)\) that is differentiable. A common choice is the sigmoid function:

\[g(\xi) = \frac{1}{1 + e^{-\xi}}\]
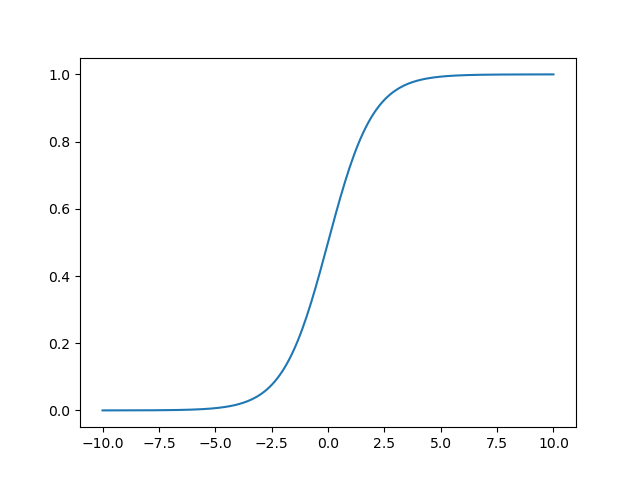
../_images/sigmoid.png

Fig. 1 The sigmoid function#

Note

There are many choices for the activation function which have different properties. Often the choice of activation function will be empirical, by experimenting with the performance of the network.

Basic algorithm#

  • Training

    • Loop over the \(T\) pairs \(({\bf x}^k, {\bf y}^k)\) for \(k = 1, \ldots, T\)

      • Predict the output for \({\bf x}^k\) as:

        \[z_i = g([{\bf A x}^k]_i) = g \left ( \sum_{j=1}^{N_\mathrm{in}} A_{ij} x^k_j \right )\]

      • Constrain that \({\bf z} = {\bf y}^k\).

        This is a minimization problem, where we are minimizing:

        \[\begin{align*} f(A_{ij}) &= \| g({\bf A x}^k) - {\bf y}^k \|^2 \\ &= \sum_{i=1}^{N_\mathrm{out}} \left [ g\left (\sum_{j=1}^{N_\mathrm{in}} A_{ij} x^k_j \right ) - y^k_i \right ]^2 \end{align*}\]

        We call this function the cost function or loss function.

        Note

        This is one possible choice for the cost function, \(f(A_{ij})\), but many others exist.

      • Update the matrix \({\bf A}\) based on the training pair \(({\bf x}^k, {\bf y^{k}})\).

  • Using the network

    With the trained \({\bf A}\), we can now use the network on data we haven’t seen before, \(\boldsymbol \chi\):

    \[z_i = g([{\bf A {\boldsymbol \chi}}^k]_i) = g \left ( \sum_{j=1}^{N_\mathrm{in}} A_{ij} \chi^k_j \right )\]

There are a lot of details that we still need to figure out involving the training and minimization. We’ll start with minimization: a common minimization technique used with neural networks is gradient descent.

Contents